La serie o sucesión de Fibonacci, es una sucesión infinita de números naturales que empieza con los términos 0 y 1, sucedidos consecutivamente por n términos, donde cada uno es la suma de los dos anteriores. Así pues, los primeros 15 términos de la serie de Fibonacci serían:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377...
Esta sucesión fue descrita en Europa por el matemático italiano Leonardo de Pisa alrededor del siglo XIII, quien también era conocido como Fibonacci. Esta sucesión tiene aplicaciones en diversos campos de la computación, las matemáticas y más increíble aún, se correlaciona con la estructura biológica de muchos seres vivos en la naturaleza.
Existen varias formas de hallar el término n de la sucesión de Fibonacci, y a partir de una de estas formas podemos obtener cada uno los anteriores términos de la serie. Así que veamos 2 de estas formas para hallar un término n de la sucesión de Fibonacci.
Primero que nada veamos la definición matemática de la sucesión de Fibonacci:
partiendo de dos primeros valores predeterminados que son:
Así pues, para hallar el sexto término de la sucesión de Fibonacci se calcularía así:
Ahora despejamos y reemplazamos cada término:
Como pudimos ver en el ejemplo, la sucesión de Fibonacci empieza a calcularse como tal a partir del término 2, ya que los primeros valores f0 y f1 están predeterminados.
Primero que nada veamos la definición matemática de la sucesión de Fibonacci:
partiendo de dos primeros valores predeterminados que son:
Así pues, para hallar el sexto término de la sucesión de Fibonacci se calcularía así:
Ahora despejamos y reemplazamos cada término:
Como pudimos ver en el ejemplo, la sucesión de Fibonacci empieza a calcularse como tal a partir del término 2, ya que los primeros valores f0 y f1 están predeterminados.
Algoritmo recursivo para calcular el término n de la sucesión de Fibonacci
Tomamos como valor de entrada la variable n
1) Si n es menor que 2, retornamos el valor de n
En el ejemplo vimos que cada término en la serie, es la suma consecutiva de los dos anteriores términos hasta llegar al segundo término. Así pues, el paso 2 sería obtener el valor de dicha suma:
2) Retornamos la suma fn-2 + fn-1
En donde cada suma es el resultado de hacer el mismo proceso desde el paso 1. Esto lo conocemos como una forma recursiva. En la siguiente gráfica podemos apreciar de forma detallada este proceso:
Complejidad de la forma recursiva
A pesar de que la forma recursiva para calcular el término n de ls sucesión de Fibonacci requiere de pocos pasos, el costo computacional es elevado, ya que es un algoritmo de orden exponencial, es decir de On. En el siguiente artículo podemos apreciar una explicación más detallada de la complejidad de los algoritmos: La complejidad de los algoritmos.
¿Y a qué se debe este nivel de complejidad?
Como podemos apreciar en la imagen, se debe a la repetición de las operaciones, la cual va creciendo exponencialmente según el término que se desea hallar. Así pues, f6 se llama una vez, f5 se llama una vez, f4 2 veces, f3 3 veces, f2 5 veces, f1 8 veces y f0 5 veces. Así pues, entre mayor sea el término a hallar, más rápido crecerán la cantidad de operaciones.
Algoritmo iterativo para calcular el término n de la sucesión de Fibonacci
Tomamos como valor de entrada la variable n
1) Declaramos tres variables de tipo entero: a, b y c. Inicializamos a con el valor 0, y b con el valor 1.
2) Iniciamos un ciclo for, el cual inicia en 0 y finaliza cuando la variable de control sea menor que n. Dentro del ciclo realizamos las siguientes acciones:
- A la variable c, le asignamos el total de la suma de a + b.
- A la variable a le asignamos el valor de b.
- A la variable b le asignamos el valor de c.
3) Al finalizar el ciclo, retornamos la variable a, la cual ha de tener el valor de fn.
Complejidad de la forma iterativa
Como podemos apreciar, la forma iterativa realiza n repeticiones donde n es el término a hallar, y en cada repetición se realizan las respectivas sumas y asignaciones de variables; por lo tanto, decimos que la forma iterativa tiene una complejidad de O(n).
Existen muchas otras formas de calcular el término n de la sucesión de Fibonacci, sin embargo, estas dos son las que estaré representando en diversos lenguajes de programación en próximas entradas.



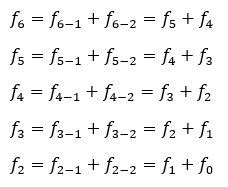
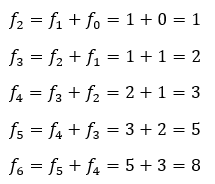







No hay comentarios.:
Publicar un comentario